Theorem 6.6- If three parallel lines intersect two transversals, then they divide the transversals proportionally.

Lines AB CD and EF are parallel. Lines GH and IJ are transversals

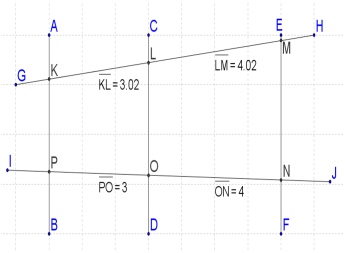
KL/PO = LM/ON
PROOF
Given: AB is parallel to CD, CD is parallel to EF
Auxiliary Line From Point K To Point N
Let Q be the intersection point of KN and LO
1. <NKM = <KNP                                           1. Alternate Interior Angles 
    <NKP = <KNM                                                 Thorem
2. Triangle KNM = Triangle NKP              2. AA similarity Postulate
3. ML/LK=NQ/QK and                                 3. Triangle Proportionality
     NO/OP=NQ/QK                                                Theorem
                                                                                        4. EC/CA=NO/OP                                            4. Transitive Property of 
                                                                                                                                                                                Congruence

---

Which statement is not true?

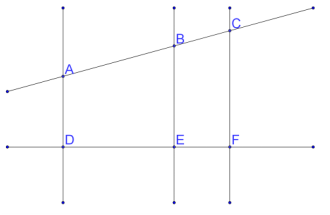
A. AB/BC=DE/EF
B. EF/DE=BC/AB
C. BC/CF=EF/CF
D. AB/AC=DE/CF
Answer: C

---